Helicidad (física de partículas)

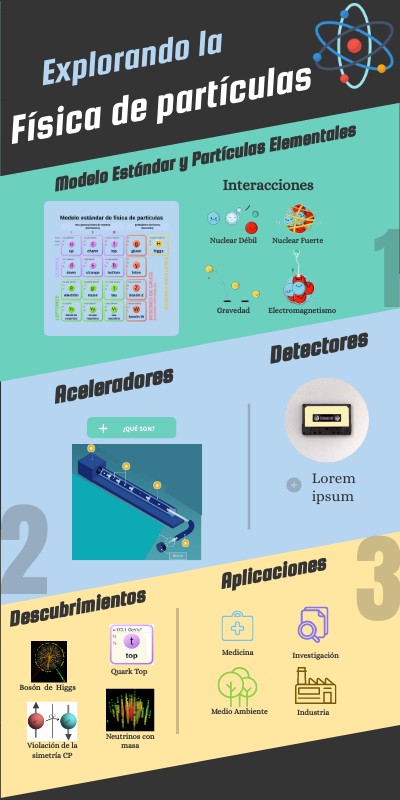
En física de partículas, la helicidad es una magnitud física asociada al espín, obtenida proyectando esa magnitud vectorial sobre la dirección de momento lineal, la definición clásica sería:

${\displaystyle h={\frac {\mathbf {S} \cdot \mathbf {p} }{\hbar \|\mathbf {p} \|}}}$

En el contexto de la física de partículas y la teoría cuántica de campos la helicidad se representa por un operador autoadjunto cuyo valor esperado viene dado por:

${\displaystyle \langle {\hat {h}}\rangle _{\psi }=\langle \psi \mid {\hat {h}}\mid \psi \rangle ={\frac {\langle \psi \mid ({\hat {S}}_{x}{\hat {p}}_{x} {\hat {S}}_{y}{\hat {p}}_{y} {\hat {S}}_{z}{\hat {p}}_{z})\mid \psi \rangle }{\hbar {\sqrt {\langle \psi \mid ({\hat {p}}_{x}^{2} {\hat {p}}_{y}^{2} {\hat {p}}_{z}^{2})\mid \psi \rangle }}}}}$

Debido a que los resultados de la medida del espín con respecto a una determinada dirección están cuantizados, es decir, sólo pueden tomar un número discreto de valores, los valores posibles de la helicidad también son discretos y por tanto la helicidad es una variable discreta. Para una partícula con espín intrínseco ${\displaystyle \scriptstyle s=(2n 1)\hbar /2}$ la helicidad puede tomar los valores ${\displaystyle \scriptstyle \{(2n 1)/2,(2n-1)/2,\dots ,-(2n-1)/2,-(2n 1)/2\}}$

Véase también

• Clasificación de Wigner
• Quiralidad